Pablo Ruiz Picasso (1881-1973) alguna vez escribió que el arte es una mentira que nos hace ver la verdad, al menos aquella que nos es dado comprender. A su vez, George Edward Pelham Box (1919-2013) escribió que todos los modelos son equivocados, pero algunos son útiles. Con este aforismo, Box quiso decir, todos los modelos están equivocados porque son una simplificación de la realidad, pero sí son útiles.
Picasso y Box eran contemporáneos, el primero considerado el pintor de mayor influencia en el siglo XX, y el segundo el estadístico de mayor influencia en el siglo XX. Ambos trataron de expresarse sobre la naturaleza, pero usando herramientas muy diferentes – Picasso realizando pinceladas sobre lienzos y Box escribiendo ecuaciones sobre papel. Dadas las diferentes formas en que trabajaron, es notable que Box y Picasso hicieran declaraciones tan similares sobre la importancia central de la abstracción para la intuición.
La abstracción juega un papel en toda iniciativa humana creativa: en el arte, la música, la literatura, la ingeniería y la ciencia. Creamos abstracciones porque nos permiten centrarnos en los elementos más importantes de un problema, aquellos relevantes para los objetivos de nuestro trabajo, sin distraernos con elementos que no son relevantes.
Modelos científicos
Los modelos científicos son, ante todo, abstracciones. Son declaraciones sobre el funcionamiento de la naturaleza que omiten deliberadamente muchos detalles y, por lo tanto, logran una comprensión que de otro modo quedaría oscurecida discursivamente. Proporcionan declaraciones inequívocas de lo que creemos que es importante.
Un principio clave en el modelado y la estadística es la necesidad de reducir las dimensiones de un problema. Un conjunto de datos puede contener mil observaciones. Al reducir sus dimensiones a un modelo con unos pocos parámetros, podemos comprenderlo mejor. Sin embargo, debido a que los modelos son abstracciones y reducen las dimensiones de un problema, debemos tratar con los elementos que elegimos omitir. Estos elementos crean incertidumbre en las predicciones de los modelos, por lo que evaluar la incertidumbre es fundamental para la ciencia.
La ciencia tendrá un impacto en la medida en que pueda hacer preguntas importantes y brindarles respuestas convincentes. Hacerlo depende de establecer una línea de inferencia que se extiende desde el pensamiento, la teoría y las preguntas actuales hasta una nueva comprensión asociada con la incertidumbre (Figura 1).

Modelos de Bayes
Científicos, periodistas, funcionarios y abogados por igual pueden afirmar correctamente que hacen afirmaciones basadas en evidencia, pero solo las declaraciones científicas incluyen evidencia asociada con la incertidumbre cuantificada. Sabemos lo que es cierto sólo en la medida en que podemos decir, con confianza, lo que es incierto. Afinar nuestro pensamiento sobre la incertidumbre y aprender a estimar adecuadamente fue el enfoque de Thomas Bayes (1702-1761) quien desarrolló el Teorema de Bayes que expresa la probabilidad condicional.
En esencia, los seguidores de la estadística tradicional solo admiten probabilidades basadas en experimentos repetibles con una confirmación empírica mientras que los llamados estadísticos bayesianos permiten probabilidades subjetivas. El Teorema sirve entonces para indicar cómo modificar nuestras probabilidades subjetivas cuando recibimos información adicional de un experimento. La estadística bayesiana está demostrando su utilidad en algunas estimaciones basadas en el conocimiento subjetivo a priori.
Los modelos Bayesianos son aplicables a una enorme variedad de problemas de investigación (finanzas, negocios, marketing, medicina, seguridad de internet, filtros spam, economía, inteligencia política y militar, industria de seguros, operaciones de búsqueda y recuperación, ambiente etc.), un enfoque que se puede entender desde los primeros principios y que se puede comunicar sin ambigüedades a otros científicos, técnicos, comunicadores, actores involucrados y tomadores de decisiones.
Las ciencias ambientales abordan una amplia variedad de problemas que requieren un enfoque interdisciplinario. Tales problemas incluyen cambios en los ecosistemas, eventos hidrológicos extremos como inundaciones o sequías, procesos terrestres como volcanismo o deslaves, contaminación del agua, suelo y aire, efectos del cambio climático global. Estos problemas se caracterizan por una gran complejidad del proceso con grandes conjuntos de datos asociados, generalmente en el espacio y el tiempo, lo que da como resultado una alta dimensionalidad de los modelos.
Aplicaciones recientes para el estudio ambiental
Un ejemplo de aplicación relativamente reciente es para evaluar la contaminación difusa en los cuerpos de agua (ríos, acuíferos, presas, esteros) por nitratos, cuyo origen puede ser la aplicación de fertilizantes, sistemas sépticos y alcantarillado, operaciones o almacenamiento de estiércol, deposición atmosférica de gas de óxido de nitrógeno principalmente del tráfico e industria, y el gas amoniaco proveniente de la agricultura.
Los nitratos amenazan los ecosistemas acuáticos y la salud humana. A menudo los nitratos en el agua se derivan de una mezcla de diferentes fuentes arriba mencionadas, pero es imposible identificar su origen y la contribución de cada fuente mediante un análisis químico convencional. Por otro lado, sería importante comprender los procesos de la contaminación difusa ya que es clave para desarrollar un plan de gestión apropiado para la protección de los recursos hídricos.
A nivel técnico, se han adoptado trazadores ambientales (sustancias o componentes introducidos por procesos naturales o el hombre) para resolver los problemas de mezcla de fuentes y comprender el origen de la contaminación del agua mediante un cálculo determinista, pero estos modelos de mezcla lineales no pueden reflejar las diversas incertidumbres involucradas en una mezcla, lo que podría dar lugar a un error en la evaluación cuantitativa.
El modelo de mezcla Bayesiano, puede ser útil en resolver esta situación, ya que puede producir la distribución de probabilidad de la contribución proporcional de cada fuente en función de las incertidumbres de los parámetros de entrada, y con eso supera las limitaciones del modelo de mezcla lineal de fuentes (Figura 2). Es más preciso y demuestra ser útil para identificar no sólo las contribuciones de la fuente dominante, sino también de otras fuentes potenciales.
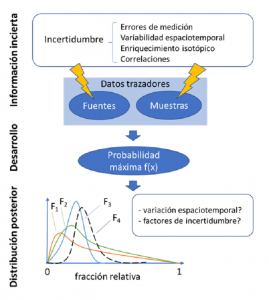
Con esta nueva herramienta es posible generar planes de gestión más adecuados – menos equivocados y más útiles en el lenguaje de Box – para proteger el ambiente, y comunicar los resultados a los actores involucrados y tomadores de decisiones de una manera cuantitativa.
Agradecimientos
Se agradece a la Comisión Nacional del Agua (CONAGUA) y Servicio de Agua y Drenaje de Monterrey (SADM) por su apoyo recibido en la recolección de información y logística de campo durante los proyectos realizados relativos al tema de este artículo. La cátedra de Economía Circular del Agua FEMSA del Tecnológico de Monterrey (ITESM) y el Consejo Nacional de Ciencia y Tecnología (CONACyT) brindaron apoyos financieros para el gasto operativo de las investigaciones, becas y estímulo del Sistema Nacional de Investigadores.
El autor
Jürgen Mahlknecht (Pertenece al Sistema Nacional de Investigadores, nivel 2; jurgen@tec.mx) es doctor en geociencias por la Universidad de Recursos Naturales y Ciencias de la Vida en Viena, Austria. Es profesor investigador del Tecnológico de Monterrey, Campus Monterrey, y coordina el Grupo de Investigación de Enfoque Estratégico Ciencia y Tecnología del Agua. Es co-líder de la cátedra de Economía Circular del Agua FEMSA del Tecnológico de Monterrey donde se tratan temas de Modelaje de los Recursos Hídricos y el Nexo Agua-Energía-Alimentos.
¿Quieres saber más?
Mahlknecht, J. (2021) Análisis de contribución de fuentes de contaminación en aguas subterráneas y superficiales utilizando el Modelo de Mezcla Bayesiano. GEOS, Vol. 41, No. 2 (2021)
Ju, Y., Mahlknecht, J., Lee, K. K., Kaown, D. (2022). Bayesian approach for simultaneous recognition of contaminant sources in groundwater and surface water resources. Current Opinion in Environmental Science & Health, 100321. https://doi.org/10.1016/j.coesh.2021.100321
Torres-Martínez, J. A., Mora, A., Knappett, P. S., Ornelas-Soto, N., Mahlknecht, J. (2020). Tracking nitrate and sulfate sources in groundwater of an urbanized valley using a multi-tracer approach combined with a Bayesian isotope mixing model. Water Research, 182, 115962. https://doi.org/10.1016/j.watres.2020.115962
Torres-Martínez, J. A., Mora, A., Mahlknecht, J., Daesslé, L. W., Cervantes-Avilés, P. A., Ledesma-Ruiz, R. (2021a). Estimation of nitrate pollution sources and transformations in groundwater of an intensive livestock-agricultural area (Comarca Lagunera), combining major ions, stable isotopes and MixSIAR model. Environmental Pollution, 269, 115445. https://doi.org/10.1016/j.envpol.2020.115445
Torres-Martínez, J. A., Mora, A., Mahlknecht, J., Kaown, D., Barceló, D. (2021b). Determining nitrate and sulfate pollution sources and transformations in a coastal aquifer impacted by seawater intrusion—A multi-isotopic approach combined with self-organizing maps and a Bayesian mixing model. Journal of Hazardous Materials, 417, 126103. https://doi.org/10.1016/j.jhazmat.2021.126103