Por David Balderas, Efraín Méndez y Pedro Ponce
En un mundo en el cual el uso de energías ha aumentado exponencialmente, el uso de métodos convencionales como el uso de combustibles fósiles se ha vuelto problemático por ser limitados y por ser altamente contaminantes. Como contraparte a las fuentes de energía convencionales, las fuentes de energía renovables son aquellas que pueden encontrarse en la naturaleza en cantidad casi ilimitadas, las cuales pueden regenerarse de manera natural o artificial y más importante que tienen un impacto en el medio ambiente es prácticamente nulo o reversible. Dentro de estas energías se encuentra la energía eólica, geotérmica, hidroeléctrica, mareomotriz, solar, etc.
Las ventajas que este tipo de energía tiene sobre las no renovables ha logrado que sean respaldadas por la comunidad internacional a través del Acuerdo de París, redactado durante la Cumbre Mundial del Clima que se realizó en 2015 en la capital francesa, el cual establece que en 2020 los 200 países firmantes reducirían sus emisiones de gases para evitar daños dramáticos del cambio climático.
Si a esto le agregamos que sus costos de producción están disminuyendo, se puede garantizar que estas energías serán parte importante del futuro, lo cual genera un creciente interés en ellas. Dentro del creciente interés por las energías renovables, la energía solar ha tomado uno de los papeles protagonistas. La energía solar requiere de sistemas fotovoltaicos que son encargados de suministrar más de 500.000 GW de la energía eléctrica consumida en todo el mundo. Por lo tanto, se han estudiado y desarrollado diferentes convertidores, algoritmos de control y técnicas para maximizar la energía recolectada por las fuentes fotovoltaicas.
Los algoritmos garantizan un comportamiento de seguimiento cuasi correcto con una baja dependencia de los parámetros de calibración, pero tienen un compromiso entre el tiempo que llegan a su punto deseado y las oscilaciones al llegar a ese estado. Sin embargo, el desempeño de una propuesta de este tipo es muy susceptible y depende de una calibración de parámetros correcta y precisa, lo que no siempre puede garantizar el comportamiento esperado.
Para poder garantizar un correcto funcionamiento se necesita de una calibración, la cual puede llegar a ser una tarea exhaustiva ya que requiere de métodos exactos o derivativos para encontrar la solución. El problema de estos métodos es que en general requieren de un trabajo enorme para la calibración, lo que finalmente se traduciría en tiempo descomunal para obtener valores óptimos. Asimismo, el uso de estos métodos evitaría poder buscar parámetros que puedan ser adaptables a condiciones inesperadas durante la ejecución.
La optimización metaheurística
Para mitigar el problema de tener que hacer una búsqueda exhaustiva, existen métodos de optimización heurística y metaheurística que, por medio de reglas de diseño inteligente de búsqueda, logran resolver un problema de búsqueda de valores óptimos, o cuando menos subóptimos, los cuales sacrifican precisión para poder encontrar un valor dentro de un tiempo viable para la ejecución. Dentro de estos algoritmos se encuentran. Cabe mencionar que estos algoritmos se emplean más frecuentemente cuando una solución aproximada es suficiente dado que la búsqueda de solución exacta requiere de un tiempo demasiado costoso.
La heurística y la metaheurística de estos algoritmos generalmente se basan en procesos naturales, como los métodos evolutivos que siguen la teoría de la evolución de Darwin, o los algoritmos de parvada, los cuales utilizan agentes que actúan como lo hacen los animales en grupo (parvadas, manadas, bancos de peces, etc.), o algoritmos que siguen procesos físicos, químicos o geográficos como método de terremotos, los cuales buscan basarse en cómo se generan los temblores y en cómo se transmiten sus ondas. Esto se muestra en la figura 1, en donde se ve cómo existen dos tipos de onda y cómo éstas mueven las partículas, ya sea a manera de compresión o de forma oscilatoria. Estas dos ondas sirvieron de base para la creación del algoritmo de terremoto.
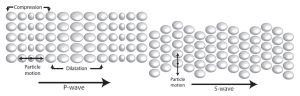
Los resultados
De esta manera, usando algoritmos de optimización se pueden hallar valores para corregir o calibrar los parámetros dentro de celdas fotovoltaicas con un comportamiento dinámico mejorado. Asimismo estos parámetros pueden modificarse de manera activa, adaptándose a varias irregularidades dentro del sistema.
Una de las características más importantes dentro de los algoritmos de optimización metaheurística es que cada algoritmo es más práctico para una solución o para otra. Por ejemplo, hay algoritmos que son mejores para la búsqueda de las mejores rutas como la optimización por colonia de hormigas. O algoritmos que son extremadamente rápidos como algoritmos por recocido simulado, pero que tienden a caer fácilmente en valores realmente alejados de lo óptimo.
De esta manera, las energías renovables pueden beneficiarse de los métodos metaheurísticos, para encontrar sus parámetros de manera eficiente y en corto tiempo, los cuales los hacen ideales para el control de algoritmos que pueden presentar cambios dinámicos dentro del control. Sin embargo, es importante realizar más pruebas para comprobar que los algoritmos trabajan de manera adecuada con sistemas fotovoltaicos.
Los autores
Dr. David Christopher Balderas Silva es profesor investigador del Tecnológico de Monterrey. Trabaja en el Grupo de Enfoque en Innovación de Productos. Entre sus intereses se encuentra la Biotecnología, la Electrónica y la Inteligencia Artificial especializándose en Optimización y Aprendizaje de Máquina (supervisada, no supervisada y aprendizaje por refuerzo). [email protected]
Dr. Pedro Ponce Cruz es profesor investigador de la Escuela de Ingeniería y Ciencias del Tecnológico de Monterrey. Pertenece al Grupo de Investigación en Innovación de Productos. Es miembro del Sistema Nacional de Investigadores, nivel 1. [email protected]
¿Quieres saber más?
Este artículo de divulgación está basado en el paper «Improved MPPT Algorithm for Photovoltaic Systems Based on the Earthquake Optimization Algorithm«, publicado en el journal Energies (Q1).
DOI: 10.3390/en13123047
















